
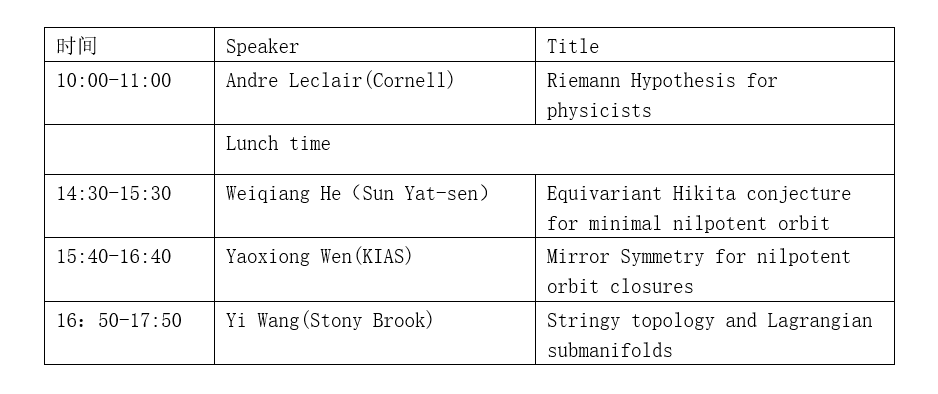
地点(Place):新葡的京集团35222vip犀浦校区综合楼403

Speaker:Andre Leclair(Cornell University)
Title:The Riemann Hypothesis for Physicists
Abstract:The Riemann Hypothesis is widely considered as the most important unsolved problem in mathematics. It has remained unsolved for over 150 years. In this colloquium I will describe two promising approaches to the problem based on ideas from physics, in particular the universal properties of brownian motion or random walks.
Speaker:Weiqiang He(Sun Yat-sen University)
Title:Equivariant Hikita conjecture for minimal nilpotent orbit
Abstract:The theory of symplectic duality is a kind of mirror symmetry in mathematical physics. Suppose two (possibly singular)manifolds are symplectic dual to each other, then there are some highly nontrivial identities betwe en the geometry and topology of them. One of them is the equivariant Hik ita conjecture. Suppose we are given a pair of symplectic dual conical sy mplectic singularities, then Hikita conjecture is a relation of the quantiz ed coordinate ring of one conical symplectic singularity to the equivariant cohomology ring of the symplectic resolution of the other dual conical sym plectic singularity. In this talk, I will focus on this case: the minimal nilpotent orbit and the slodowy slice of the subregular orbit. This is a joint work with Xiaojun Chen and Sirui Yu.
Speaker:Yaoxiong Wen(KIAS)
Title:Mirror symmetry for nilpotent orbit closure
Abstract:Inspired by the work of Gukov-Witten, we investigate stringy Epolynomials of nilpotent orbit closures of type $B_n$ and $C_n$.Classically, there is a famous Springer duality between special orbits. Therefore,it is natural to speculate that the mirror symmetry we seek may coincide with Springer duality in the context of special orbits. Unfortunately, such a naive statement fails. To remedy the situation, we propose a conjecture which asserts the mirror symmetry for certain parabolic/induced covers of s pecial orbits. Then, we prove the conjecture for Richardson orbits and obt ain certain partial results in general. In the mirror symmetry, we find an interesting seesaw phenomenon where Lusztig's canonical quotient group plays an important role. This talk is based on the joint work with Baohua Fu and Yongbin Ruan,https://arxiv.org/abs/2207.10533.
报告人:王怡(纽约州立大学石溪分校)题目:弦拓扑和拉格朗日子流形
摘要:Chas和Sullivan在1999年发现,流形上环路的不同相交方式可以诱导出自由环路空间(free loop space)的同调群上丰富的代数结构,由此开拓出了弦拓扑(s tring topology)这一领域。Fukaya及其合作者在2000年左右研究了一般情形下辛流形中拉格朗日子流形(Lagrangian submanifold)相交的Floer理论,特别地,每个拉格朗日子流形都给出了一个A-无穷代数,其中蕴含了边界落在该子流形上的伪全纯圆盘(pseudo-holomorphic disk)映射的信息。在今天的报告中,基于Fukaya、Irie和我自己的工作,我将阐释两者的联系。我将从Gromov证明C^n中不存在第一贝蒂数为零的紧致无边拉格朗日子流形讲起。


